TRADERS’ TIPS
February 2025

For this month’s Traders’ Tips, the focus is John F. Ehlers’ article in this issue, “Drunkard’s Walk: Theory And Measurement By Autocorrelation.” Here, we present the February 2025 Traders’ Tips code with possible implementations in various software.
You can right-click on any chart to open it in a new tab or window and view it at it’s originally supplied size, often much larger than the version printed in the magazine.
The Traders’ Tips section is provided to help the reader implement a selected technique from an article in this issue or another recent issue. The entries here are contributed by software developers or programmers for software that is capable of customization.

TradeStation: February 2025
John Ehlers’ new autocorrelation indicator, introduced in this article in this issue (“Drunkard’s Walk: Theory And Measurement By Autocorrelation”) can be used to identify patterns in financial markets, which often behave unpredictably, like a “drunkard’s walk.” This indicator draws upon mathematical models—the diffusion equation for trends and the wave equation for cycles—to uncover hidden order within seemingly random price movements. By analyzing the correlation of price data over different periods, the indicator can be used to reveal cyclical patterns, potential reversals, and emerging trends.
Function: $SuperSmoother
{
SuperSmoother Function
(C) 2004-2024 John F. Ehlers
}
inputs:
Price(numericseries),
Period(numericsimple);
variables:
a1( 0 ),
b1( 0 ),
c1( 0 ),
c2( 0 ),
c3( 0 );
a1 = ExpValue(-1.414 * 3.14159 / Period);
b1 = 2 * a1 * Cosine(1.414 * 180 / Period);
c2 = b1;
c3 = -a1 * a1;
c1 = 1 - c2 - c3;
if CurrentBar >= 4 then
$SuperSmoother = c1*(Price + Price[1]) / 2
+ c2 * $SuperSmoother[1] + c3 * $SuperSmoother[2];
if CurrentBar < 4 then
$SuperSmoother = Price;
Indicator: Autocorrelation
{
TASC FEB 2025
AutoCorrelation Indicator
(C) 2024 John F. Ehlers
}
inputs:
Length( 20 );
variables:
Filt( 0 ),
Lag( 0 ),
J( 0 ),
Sx( 0 ),
Sy( 0 ),
Sxx( 0 ),
Sxy( 0 ),
Syy( 0 ),
X( 0 ),
Y( 0 ),
Color1( 0 ),
Color2( 0 );
arrays:
Corr[100]( 0 );
Filt = $UltimateSmoother( Close, 20 );
// Cycle test waveform
// Filt = Sine(360*CurrentBar / 20);
// >>>>>>>>> Correlation >>>>>>>>>>>>
for Lag = 0 to 99
begin
Sx = 0;
Sy = 0;
Sxx = 0;
Sxy = 0;
Syy = 0;
for J = 0 to Length - 1
begin
X = Filt[J];
Y = Filt[Lag + J];
Sx = Sx + X;
Sy = Sy + Y;
Sxx = Sxx + X*X;
Sxy = Sxy + X*Y;
Syy = Syy + Y*Y;
end;
If (Length*Sxx - Sx*Sx > 0) and (Length*Syy - Sy*Sy > 0) Then
Corr[Lag + 1] = (Length*Sxy - Sx*Sy) / SquareRoot((Length*Sxx -
Sx*Sx)*(Length*Syy - Sy*Sy));
end;
//Plot the AutoCorrelation as a Heatmap
for Lag = 1 to 99
begin
//Convert Power to RGB Color for Display
if Corr[Lag + 1] >= 0 Then
begin
Color2 = 255;
Color1 = 255*(1 - Corr[Lag + 1]);
end;
if Corr[Lag + 1] < 0 then
begin
Color2 = 255*(1 + Corr[Lag + 1]);
Color1 = 255;
end;
switch( Lag )
begin
case 0:
Plot1(0, "S0", RGB(Color1, Color2, 0),0,4);
case 1:
Plot2(1, "S1", RGB(Color1, Color2, 0),0,4);
end;
switch( Lag )
begin
case 0:
Plot1(0, "S0", RGB(Color1, Color2, 0), 0, 4);
case 1:
Plot2(1, "S1", RGB(Color1, Color2, 0), 0, 4);
case 2:
Plot3(2, "S2", RGB(Color1, Color2, 0), 0, 4);
case 3:
Plot4(3, "S3", RGB(Color1, Color2, 0), 0, 4);
case 4:
Plot5(4, "S4", RGB(Color1, Color2, 0), 0, 4);
case 5:
Plot6(5, "S5", RGB(Color1, Color2, 0), 0, 4);
case 6:
Plot7(6, "S6", RGB(Color1, Color2, 0), 0, 4);
case 7:
Plot8(7, "S7", RGB(Color1, Color2, 0), 0, 4);
case 8:
Plot9(8, "S8", RGB(Color1, Color2, 0), 0, 4);
case 9:
Plot10(9, "S9", RGB(Color1, Color2, 0), 0, 4);
case 10:
Plot11(10, "S10", RGB(Color1, Color2, 0), 0, 4);
case 11:
Plot12(11, "S11", RGB(Color1, Color2, 0), 0, 4);
case 12:
Plot13(12, "S12", RGB(Color1, Color2, 0), 0, 4);
case 13:
Plot14(13, "S13", RGB(Color1, Color2, 0), 0, 4);
case 14:
Plot15(14, "S14", RGB(Color1, Color2, 0), 0, 4);
case 15:
Plot16(15, "S15", RGB(Color1, Color2, 0), 0, 4);
case 16:
Plot17(16, "S16", RGB(Color1, Color2, 0), 0, 4);
case 17:
Plot18(17, "S17", RGB(Color1, Color2, 0), 0, 4);
case 18:
Plot19(18, "S18", RGB(Color1, Color2, 0), 0, 4);
case 19:
Plot20(19, "S19", RGB(Color1, Color2, 0), 0, 4);
case 20:
Plot21(20, "S20", RGB(Color1, Color2, 0), 0, 4);
case 21:
Plot22(21, "S21", RGB(Color1, Color2, 0), 0, 4);
case 22:
Plot23(22, "S22", RGB(Color1, Color2, 0), 0, 4);
case 23:
Plot24(23, "S23", RGB(Color1, Color2, 0), 0, 4);
case 24:
Plot25(24, "S24", RGB(Color1, Color2, 0), 0, 4);
case 25:
Plot26(25, "S25", RGB(Color1, Color2, 0), 0, 4);
case 26:
Plot27(26, "S26", RGB(Color1, Color2, 0), 0, 4);
case 27:
Plot28(27, "S27", RGB(Color1, Color2, 0), 0, 4);
case 28:
Plot29(28, "S28", RGB(Color1, Color2, 0), 0, 4);
case 29:
Plot30(29, "S29", RGB(Color1, Color2, 0), 0, 4);
case 30:
Plot31(30, "S30", RGB(Color1, Color2, 0), 0, 4);
case 31:
Plot32(31, "S31", RGB(Color1, Color2, 0), 0, 4);
case 32:
Plot33(32, "S32", RGB(Color1, Color2, 0), 0, 4);
case 33:
Plot34(33, "S33", RGB(Color1, Color2, 0), 0, 4);
case 34:
Plot35(34, "S34", RGB(Color1, Color2, 0), 0, 4);
case 35:
Plot36(35, "S35", RGB(Color1, Color2, 0), 0, 4);
case 36:
Plot37(36, "S36", RGB(Color1, Color2, 0), 0, 4);
case 37:
Plot38(37, "S37", RGB(Color1, Color2, 0), 0, 4);
case 38:
Plot39(38, "S38", RGB(Color1, Color2, 0), 0, 4);
case 39:
Plot40(39, "S39", RGB(Color1, Color2, 0), 0, 4);
case 40:
Plot41(40, "S40", RGB(Color1, Color2, 0), 0, 4);
case 41:
Plot42(41, "S41", RGB(Color1, Color2, 0), 0, 4);
case 42:
Plot43(42, "S42", RGB(Color1, Color2, 0), 0, 4);
case 43:
Plot44(43, "S43", RGB(Color1, Color2, 0), 0, 4);
case 44:
Plot45(44, "S44", RGB(Color1, Color2, 0), 0, 4);
case 45:
Plot46(45, "S45", RGB(Color1, Color2, 0), 0, 4);
case 46:
Plot47(46, "S46", RGB(Color1, Color2, 0), 0, 4);
case 47:
Plot48(47, "S47", RGB(Color1, Color2, 0), 0, 4);
case 48:
Plot49(48, "S48", RGB(Color1, Color2, 0), 0, 4);
case 49:
Plot50(49, "S49", RGB(Color1, Color2, 0), 0, 4);
case 50:
Plot51(50, "S50", RGB(Color1, Color2, 0), 0, 4);
case 51:
Plot52(51, "S51", RGB(Color1, Color2, 0), 0, 4);
case 52:
Plot53(52, "S52", RGB(Color1, Color2, 0), 0, 4);
case 53:
Plot54(53, "S53", RGB(Color1, Color2, 0), 0, 4);
case 54:
Plot55(54, "S54", RGB(Color1, Color2, 0), 0, 4);
case 55:
Plot56(55, "S55", RGB(Color1, Color2, 0), 0, 4);
case 56:
Plot57(56, "S56", RGB(Color1, Color2, 0), 0, 4);
case 57:
Plot58(57, "S57", RGB(Color1, Color2, 0), 0, 4);
case 58:
Plot59(58, "S58", RGB(Color1, Color2, 0), 0, 4);
case 59:
Plot60(59, "S59", RGB(Color1, Color2, 0), 0, 4);
case 60:
Plot61(60, "S60", RGB(Color1, Color2, 0), 0, 4);
case 61:
Plot62(61, "S61", RGB(Color1, Color2, 0), 0, 4);
case 62:
Plot63(62, "S62", RGB(Color1, Color2, 0), 0, 4);
case 63:
Plot64(63, "S63", RGB(Color1, Color2, 0), 0, 4);
case 64:
Plot65(64, "S64", RGB(Color1, Color2, 0), 0, 4);
case 65:
Plot66(65, "S65", RGB(Color1, Color2, 0), 0, 4);
case 66:
Plot67(66, "S66", RGB(Color1, Color2, 0), 0, 4);
case 67:
Plot68(67, "S67", RGB(Color1, Color2, 0), 0, 4);
case 68:
Plot69(68, "S68", RGB(Color1, Color2, 0), 0, 4);
case 69:
Plot70(69, "S69", RGB(Color1, Color2, 0), 0, 4);
case 70:
Plot71(70, "S70", RGB(Color1, Color2, 0), 0, 4);
case 71:
Plot72(71, "S71", RGB(Color1, Color2, 0), 0, 4);
case 72:
Plot73(72, "S72", RGB(Color1, Color2, 0), 0, 4);
case 73:
Plot74(73, "S73", RGB(Color1, Color2, 0), 0, 4);
case 74:
Plot75(74, "S74", RGB(Color1, Color2, 0), 0, 4);
case 75:
Plot76(75, "S75", RGB(Color1, Color2, 0), 0, 4);
case 76:
Plot77(76, "S76", RGB(Color1, Color2, 0), 0, 4);
case 77:
Plot78(77, "S77", RGB(Color1, Color2, 0), 0, 4);
case 78:
Plot79(78, "S78", RGB(Color1, Color2, 0), 0, 4);
case 79:
Plot80(79, "S79", RGB(Color1, Color2, 0), 0, 4);
case 80:
Plot81(80, "S80", RGB(Color1, Color2, 0), 0, 4);
case 81:
Plot82(81, "S81", RGB(Color1, Color2, 0), 0, 4);
case 82:
Plot83(82, "S82", RGB(Color1, Color2, 0), 0, 4);
case 83:
Plot84(83, "S83", RGB(Color1, Color2, 0), 0, 4);
case 84:
Plot85(84, "S84", RGB(Color1, Color2, 0), 0, 4);
case 85:
Plot86(85, "S85", RGB(Color1, Color2, 0), 0, 4);
case 86:
Plot87(86, "S86", RGB(Color1, Color2, 0), 0, 4);
case 87:
Plot88(87, "S87", RGB(Color1, Color2, 0), 0, 4);
case 88:
Plot89(88, "S88", RGB(Color1, Color2, 0), 0, 4);
case 89:
Plot90(89, "S89", RGB(Color1, Color2, 0), 0, 4);
case 90:
Plot91(90, "S90", RGB(Color1, Color2, 0), 0, 4);
case 91:
Plot92(91, "S91", RGB(Color1, Color2, 0), 0, 4);
case 92:
Plot93(92, "S92", RGB(Color1, Color2, 0), 0, 4);
case 93:
Plot94(93, "S93", RGB(Color1, Color2, 0), 0, 4);
case 94:
Plot95(94, "S94", RGB(Color1, Color2, 0), 0, 4);
case 95:
Plot96(95, "S95", RGB(Color1, Color2, 0), 0, 4);
case 96:
Plot97(96, "S96", RGB(Color1, Color2, 0), 0, 4);
case 97:
Plot98(97, "S97", RGB(Color1, Color2, 0), 0, 4);
case 98:
Plot99(98, "S98", RGB(Color1, Color2, 0), 0, 4);
end;
end;
A sample chart is shown in Figure 1.
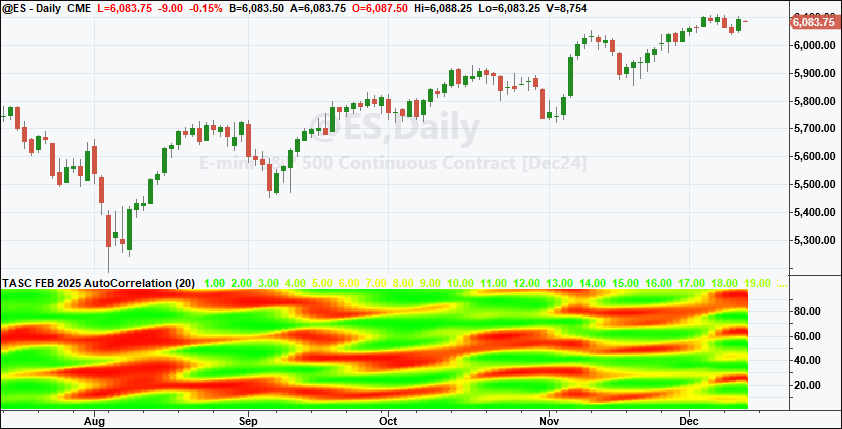
FIGURE 1: TRADESTATION. This daily chart of the continuous contract emini S&P 500 futures shows a portion of 2024 with the indicator applied using a length of 20.
This article is for informational purposes. No type of trading or investment recommendation, advice, or strategy is being made, given, or in any manner provided by TradeStation Securities or its affiliates.
—John Robinson
TradeStation Securities, Inc.
www.TradeStation.com
BACK TO LIST

Wealth-Lab.com: February 2025
So...a Z-transform and a LaPlace transform walked into a smokey bar and began solving the continuous variable random walk problem with differential and wave equations. They stumbled out in a drunkard’s walk...
In the article “Drunkard’s Walk: Theory And Measurement By Autocorrelation” in this issue, John Ehlers presents coding for his autocorrelation indicator and heatmap display. WealthLab’s version of that code is presented here, with the result given in Figure 2.
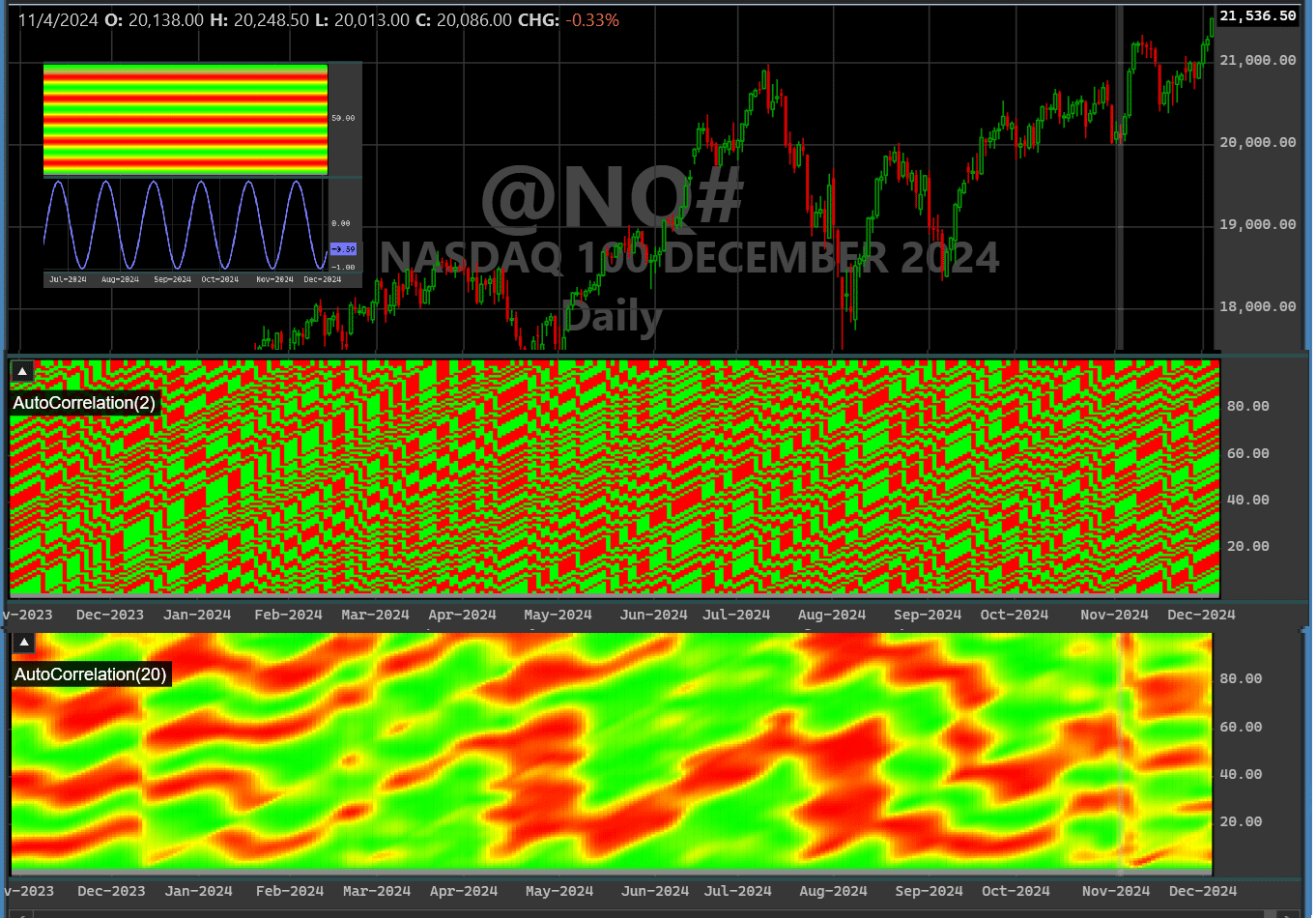
FIGURE 2: WEALTH-LAB. Here’s an example periodogram displaying autocorrelation in the S&P emini futures, using length=2 and 20 bars.
We find that the 2-period autocorrelation is quick to predict reversals and may produce many false alarms.
using WealthLab.Backtest;
using System;
using WealthLab.Core;
using WealthLab.Indicators;
using WealthLab.TASC;
namespace WealthScript6
{
public class DrunkardAutoCorr : UserStrategyBase
{
Parameter _period;
Parameter _testWave;
public DrunkardAutoCorr()
{
_period = AddParameter("Period", ParameterType.Int32, 20, 5, 60, 1);
_testWave = AddParameter("Sine Test", ParameterType.Int32, 0, 0, 1);
}
public override void Initialize(BarHistory bars)
{
int length = _period.AsInt;
double[] corr = new double[101];
TimeSeries[] raster = new TimeSeries[101];
for (int n = 0; n < 101; n++)
{
raster[n] = new TimeSeries(bars.DateTimes, n);
PlotTimeSeriesLine(raster[n], "", "A/C", WLColor.Black, 4, suppressLabels: true);
}
DrawHeaderText($"AutoCorrelation({length})", WLColor.White, 12, "A/C");
SetPaneDrawingOptions("A/C", 40);
TimeSeries _filt = UltimateSmoother.Series(bars.Close, _period.AsInt);
//Cycle test waveform
if (_testWave.AsInt == 1)
{
_filt = new TimeSeries(bars.DateTimes);
for (int n = 0; n < bars.Count; n++)
_filt[n] = Math.Sin(2 * Math.PI * n / 20);
PlotTimeSeriesLine(_filt, "Sine", "Sine");
}
for (int bar = length + 100; bar < bars.Count; bar++)
{
//>>>>>>>>> Correlation >>>>>>>>>>>>
for (int lag = 0; lag < 100; lag++)
{
double Sx = 0, Sy = 0, Sxx = 0, Sxy = 0, Syy = 0;
for (int j = 0; j < length; j++)
{
double X = _filt[bar - j];
double Y = _filt[bar - (lag + j)];
Sx = Sx + X;
Sy = Sy + Y;
Sxx = Sxx + X * X;
Sxy = Sxy + X * Y;
Syy = Syy + Y * Y;
}
if (length * Sxx - Sx * Sx > 0 && length * Syy - Sy * Sy > 0)
corr[lag + 1] = (length * Sxy - Sx * Sy) / Math.Sqrt((length * Sxx - Sx * Sx) * (length * Syy - Sy * Sy));
}
//convert AutoCorrelation to colors
for (int lag = 1; lag < 100; lag++)
{
byte clr1 = 255;
byte clr2 = 255;
if (corr[lag + 1] >= 0)
clr1 = (byte)(255 * (1 - corr[lag + 1]));
else
clr2 = (byte)(255 * (1 + corr[lag + 1]));
SetSeriesBarColor(raster[lag + 1], bar, WLColor.FromRgb(clr1, clr2, 0));
}
}
}
public override void Execute(BarHistory bars, int idx)
{ }
}
}
—Robert Sucher
Wealth-Lab team
www.wealth-lab.com
BACK TO LIST
TradingView: February 2025
The TradingView Pine Script code presented here implements John Ehlers’ autocorrelation indicator, introduced in his article in this issue titled “Drunkard’s Walk: Theory And Measurement By Autocorrelation.”
// TASC Issue: February 2025
// Article: Drunkard's Walk:
// Theory And Measurement By Autocorrelation.
// Article By: John F. Elhers
// Language: TradingView's Pine Script™ v5
// Provided By: PineCoders, for tradingview.com
//@version=5
title ='TASC 2025.02 Autocorrelation Indicator'
stitle = 'ACI'
indicator(title, stitle, false)
// --- Inputs and Constants ---
//@enum Range Selection Enumeration:
enum R
R1 = '0 -> 32'
R2 = '33 -> 65'
R3 = '66 -> 98'
// @variable Full Angle Rotation `360`.
float FROT = 2.0 * math.pi
// @variable Square Root of 2 `1.414`.
float SQRT2 = math.sqrt(2.0)
// @variable Perfect Cycle Test signal.
// `Signal = math.sin(360.0 * bar_index / 30.0)`.
float TS = math.sin(FROT * bar_index / 30.0)
float Src = input.source(close, 'Source:')
int Length = input.int(100, 'Length:')
// @variable Use Test Signal.
bool iTest = input.bool(false, 'Use Test Signal:')
// @variable Range Selection.
R iR = input.enum(R.R1, 'Range Selection:')
// --- Functions ---
// @function UltimateSmoother
UltimateSmoother (float src, int period) =>
float a1 = math.exp(-1.414 * math.pi / period)
float c2 = 2.0 * a1 * math.cos(1.414 * math.pi / period)
float c3 = -a1 * a1
float c1 = (1.0 + c2 - c3) / 4.0
float us = src
if bar_index >= 4
us := (1.0 - c1) * src +
(2.0 * c1 - c2) * src[1] -
(c1 + c3) * src[2] +
c2 * nz(us[1]) + c3 * nz(us[2])
us
// @function Correlation
correlation (float src, int length) =>
float[] _corr = array.new<float>(101, 0.0)
color[] _col = array.new<color>(101, #00000000)
for _l = 0 to 99
float _Sx = 0.0
float _Sy = 0.0
float _Sxx = 0.0
float _Sxy = 0.0
float _Syy = 0.0
for _j = 0 to length - 1
float _x = src[_j]
float _y = src[_l + _j]
_Sx += _x
_Sy += _y
_Sxx += _x * _x
_Sxy += _x * _y
_Syy += _y * _y
float _ca1 = length * _Sxx - _Sx * _Sx
float _ca2 = length * _Syy - _Sy * _Sy
if _ca1 > 0.0 and _ca2 > 0.0
float _ca3 = length * _Sxy - _Sx * _Sy
_corr.set(_l + 1, _ca3 / math.sqrt(_ca1 * _ca2))
for _l = 1 to 99
float _c = _corr.get(_l + 1)
if _c >= 0.0
_col.set(_l, color.rgb(255, 255 * (1.0 - _c), 0))
if _c < 0.0
_col.set(_l, color.rgb(255 * (1.0 + _c), 255, 0))
_col
// --- Calculations: ---
float Filt = iTest ? TS : UltimateSmoother(Src, Length)
//@variable Color array.
color[] C = correlation(Filt, Length)
switch iR
R.R1 => C := C.slice(0, 32)
R.R2 => C := C.slice(33, 65)
=> C := C.slice(66, 98)
int IDX00 = iR == R.R1 ? 00 : (iR == R.R2 ? 33+00 : 66+00)
int IDX01 = iR == R.R1 ? 01 : (iR == R.R2 ? 33+01 : 66+01)
int IDX02 = iR == R.R1 ? 02 : (iR == R.R2 ? 33+02 : 66+02)
int IDX03 = iR == R.R1 ? 03 : (iR == R.R2 ? 33+03 : 66+03)
int IDX04 = iR == R.R1 ? 04 : (iR == R.R2 ? 33+04 : 66+04)
int IDX05 = iR == R.R1 ? 05 : (iR == R.R2 ? 33+05 : 66+05)
int IDX06 = iR == R.R1 ? 06 : (iR == R.R2 ? 33+06 : 66+06)
int IDX07 = iR == R.R1 ? 07 : (iR == R.R2 ? 33+07 : 66+07)
int IDX08 = iR == R.R1 ? 08 : (iR == R.R2 ? 33+08 : 66+08)
int IDX09 = iR == R.R1 ? 09 : (iR == R.R2 ? 33+09 : 66+09)
int IDX10 = iR == R.R1 ? 10 : (iR == R.R2 ? 33+10 : 66+10)
int IDX11 = iR == R.R1 ? 11 : (iR == R.R2 ? 33+11 : 66+11)
int IDX12 = iR == R.R1 ? 12 : (iR == R.R2 ? 33+12 : 66+12)
int IDX13 = iR == R.R1 ? 13 : (iR == R.R2 ? 33+13 : 66+13)
int IDX14 = iR == R.R1 ? 14 : (iR == R.R2 ? 33+14 : 66+14)
int IDX15 = iR == R.R1 ? 15 : (iR == R.R2 ? 33+15 : 66+15)
int IDX16 = iR == R.R1 ? 16 : (iR == R.R2 ? 33+16 : 66+16)
int IDX17 = iR == R.R1 ? 17 : (iR == R.R2 ? 33+17 : 66+17)
int IDX18 = iR == R.R1 ? 18 : (iR == R.R2 ? 33+18 : 66+18)
int IDX19 = iR == R.R1 ? 19 : (iR == R.R2 ? 33+19 : 66+19)
int IDX20 = iR == R.R1 ? 20 : (iR == R.R2 ? 33+20 : 66+20)
int IDX21 = iR == R.R1 ? 21 : (iR == R.R2 ? 33+21 : 66+21)
int IDX22 = iR == R.R1 ? 22 : (iR == R.R2 ? 33+22 : 66+22)
int IDX23 = iR == R.R1 ? 23 : (iR == R.R2 ? 33+23 : 66+23)
int IDX24 = iR == R.R1 ? 24 : (iR == R.R2 ? 33+24 : 66+24)
int IDX25 = iR == R.R1 ? 25 : (iR == R.R2 ? 33+25 : 66+25)
int IDX26 = iR == R.R1 ? 26 : (iR == R.R2 ? 33+26 : 66+26)
int IDX27 = iR == R.R1 ? 27 : (iR == R.R2 ? 33+27 : 66+27)
int IDX28 = iR == R.R1 ? 28 : (iR == R.R2 ? 33+28 : 66+28)
int IDX29 = iR == R.R1 ? 29 : (iR == R.R2 ? 33+29 : 66+29)
int IDX30 = iR == R.R1 ? 30 : (iR == R.R2 ? 33+30 : 66+30)
int IDX31 = iR == R.R1 ? 31 : (iR == R.R2 ? 33+31 : 66+31)
int IDX32 = iR == R.R1 ? 32 : (iR == R.R2 ? 33+32 : 66+32)
PLTS = plot.style_line, DSP = display.pane, F = false
plot(IDX01, 'S', C.get(00), 2, PLTS, F, display=DSP)
plot(IDX02, 'S', C.get(01), 2, PLTS, F, display=DSP)
plot(IDX03, 'S', C.get(02), 2, PLTS, F, display=DSP)
plot(IDX04, 'S', C.get(03), 2, PLTS, F, display=DSP)
plot(IDX05, 'S', C.get(04), 2, PLTS, F, display=DSP)
plot(IDX06, 'S', C.get(05), 2, PLTS, F, display=DSP)
plot(IDX07, 'S', C.get(06), 2, PLTS, F, display=DSP)
plot(IDX08, 'S', C.get(07), 2, PLTS, F, display=DSP)
plot(IDX09, 'S', C.get(08), 2, PLTS, F, display=DSP)
plot(IDX10, 'S', C.get(09), 2, PLTS, F, display=DSP)
plot(IDX11, 'S', C.get(10), 2, PLTS, F, display=DSP)
plot(IDX12, 'S', C.get(11), 2, PLTS, F, display=DSP)
plot(IDX13, 'S', C.get(12), 2, PLTS, F, display=DSP)
plot(IDX14, 'S', C.get(13), 2, PLTS, F, display=DSP)
plot(IDX15, 'S', C.get(14), 2, PLTS, F, display=DSP)
plot(IDX16, 'S', C.get(15), 2, PLTS, F, display=DSP)
plot(IDX17, 'S', C.get(16), 2, PLTS, F, display=DSP)
plot(IDX18, 'S', C.get(17), 2, PLTS, F, display=DSP)
plot(IDX19, 'S', C.get(18), 2, PLTS, F, display=DSP)
plot(IDX20, 'S', C.get(19), 2, PLTS, F, display=DSP)
plot(IDX21, 'S', C.get(20), 2, PLTS, F, display=DSP)
plot(IDX22, 'S', C.get(21), 2, PLTS, F, display=DSP)
plot(IDX23, 'S', C.get(22), 2, PLTS, F, display=DSP)
plot(IDX24, 'S', C.get(23), 2, PLTS, F, display=DSP)
plot(IDX25, 'S', C.get(24), 2, PLTS, F, display=DSP)
plot(IDX26, 'S', C.get(25), 2, PLTS, F, display=DSP)
plot(IDX27, 'S', C.get(26), 2, PLTS, F, display=DSP)
plot(IDX28, 'S', C.get(27), 2, PLTS, F, display=DSP)
plot(IDX29, 'S', C.get(28), 2, PLTS, F, display=DSP)
plot(IDX30, 'S', C.get(29), 2, PLTS, F, display=DSP)
plot(IDX31, 'S', C.get(30), 2, PLTS, F, display=DSP)
plot(IDX32, 'S', C.get(31), 2, PLTS, F, display=DSP)
An example chart is shown in Figure 3.
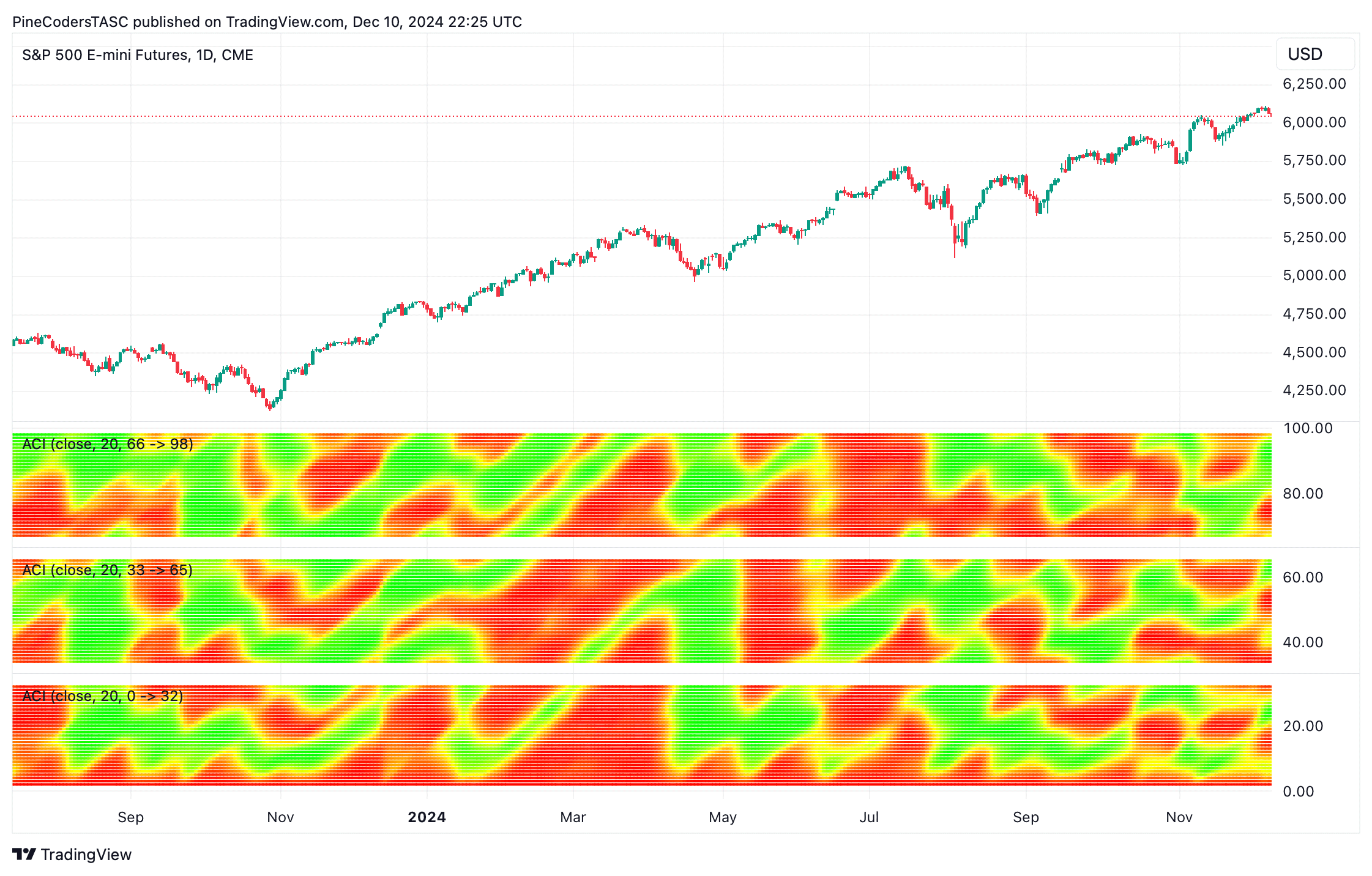
FIGURE 3: TRADINGVIEW. Here you see an example periodogram of Ehlers’ autocorrelation indicator on the emini S&P 500 futures market.
The indicator is available on TradingView from the PineCodersTASC account at https://www.tradingview.com/u/PineCodersTASC/#published-scripts.
—PineCoders, for TradingView
www.TradingView.com
BACK TO LIST

Neuroshell Trader: February 2025
In “Drunkard’s Walk: Theory And Measurement By Autocorrelation” in this issue, John Ehlers introduces his autocorrelation indicator displayed on a periodogram. Ehlers designed the approach he describes in the article to help to analyze price data over different periods.
This type of sliding window correlation can be easily implemented in NeuroShell Trader. Simply select “New indicator ...” from the insert menu and use the indicator wizard to create the indicator. Note that by entering a parameter value of 0:99, NeuroShell Trader will automatically insert the correlation with lags between 0 and 99 in one single step onto your NeuroShell Trader chart:
LinXYReg r( UltimateSmoother(Close,20), Lag(UltimateSmoother(Close,20),0:99),20)
Users of NeuroShell Trader can go to the Stocks & Commodities section of the NeuroShell Trader free technical support website to download a copy of this or any previous Traders’ Tips.
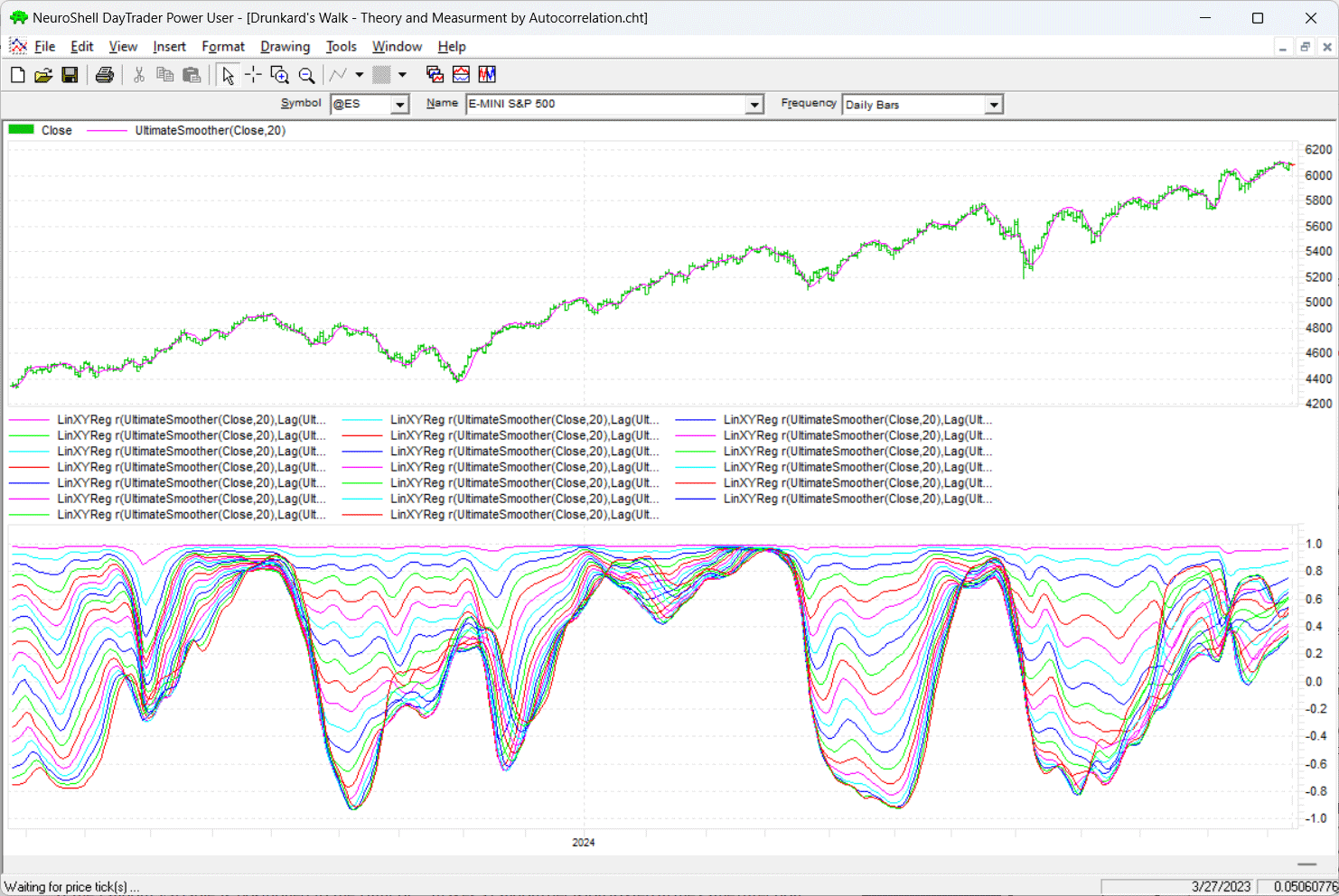
FIGURE 4: NEUROSHELL TRADER. This NeuroShell Trader chart demonstrates the sliding window correlations of the UltimateSmoother on emini Nasdaq-100 data.
—Ward Systems Group, Inc.
sales@wardsystems.com
www.neuroshell.com
BACK TO LIST

The Zorro Project: February 2025
John Ehlers’ article in this issue, “Drunkard’s Walk: Theory And Measurement By Autocorrelation,” deals with the usage of price autocorrelation for trading. Autocorrelation can be found in real price curves but is not found in completely random data. Depending on market regime, prices correlate with themselves shifted by some lag into the past. This is caused by some cyclic behavior of price curves, and can be used for trading systems.
In his EasyLanguage script, Ehlers generates an autocorrelation heatmap over a lag range from 1 to 100. He is not using raw price data, but rather, filters it beforehand with his UltimateSmoother. That filter was the topic of a past S&C article by Ehlers and the accompanying Traders’ Tips section, so I already coded it. Here again is the code for the UltimateSmoother, in C:
var UltimateSmoother (var *Data, int Length)
{
var f = (1.414*PI) / Length;
var a1 = exp(-f);
var c2 = 2*a1*cos(f);
var c3 = -a1*a1;
var c1 = (1+c2-c3)/4;
vars US = series(*Data,4);
return US[0] = (1-c1)*Data[0] + (2*c1-c2)*Data[1] - (c1+c3)*Data[2]
+ c2*US[1] + c3*US[2];
}
Next, we can replicate Ehlers’ autocorrelation heatmap from his article in this issue. His script plots every pixel of the heatmap in a separate function. The Zorro platform provides heatmap and contour plots as part of its advanced plotting functions. This results in somewhat simpler and shorter code:
void run()
{
BarPeriod = 1440;
StartDate = 20231001;
EndDate = 20240901;
LookBack = 150;
assetAdd("SPY","STOOQ:SPY.US");
asset("SPY");
int Lag, Length = 20;
vars Prices = series(SmoothUltimate(seriesC(),Length));
if(!is(LOOKBACK))
for(Lag=1; Lag<100; Lag++) {
int Row = dataRow(1,dataAppendRow(1,3));
dataSet(1,Row,0,Correlation(Prices+Length,Prices+Length+Lag,Length));
dataSet(1,Row,1,wdate());
dataSet(1,Row,2,(var)Lag);
}
if(is(EXITRUN))
dataChart(1,0,CONTOUR,NULL);}
In this code, we’re storing the correlation value, the date, and the lag in a dataset. For the correlation, we’re using the Pearson correlation function. The resulting heatmap replicates the chart in Ehlers’ article, but I think it looks a bit prettier! (See Figure 5).
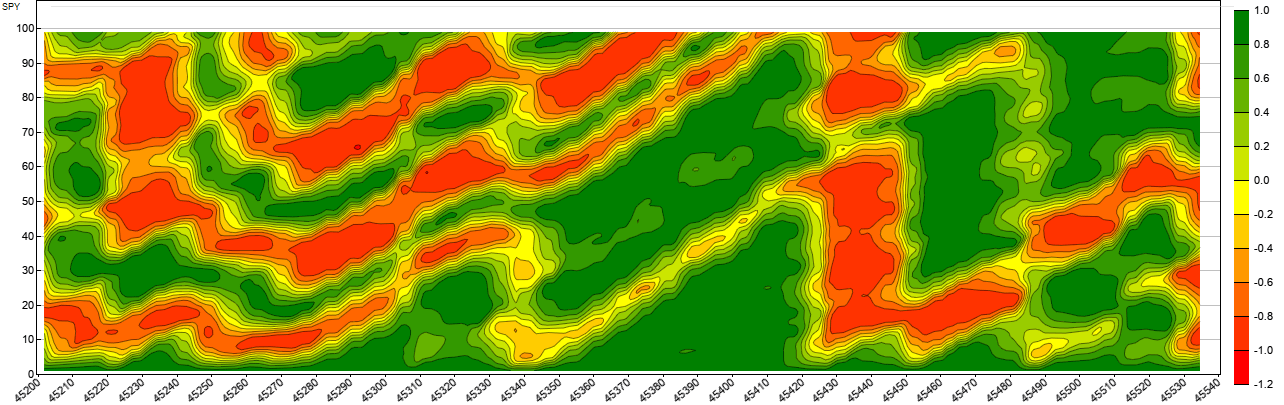
FIGURE 5: ZORRO. Here is an example of autocorrelation and periodic patterns in SPY price data. The y-axis is the lag and the x-axis represents the date (in the Windows date format). Green areas show strong correlation while red areas show strong anticorrelation.
The y-axis is the lag, and the x-axis is the date in the Windows DATE format, which is simply the number of days since 1899. Green areas have strong correlation, while the red areas show strong anticorrelation. We can see from the periodic patterns that the SPY price curve indeed has cyclic components which allow, to some degree, the prediction of short-term price trends.
The code can be downloaded from the 2024 script repository on https://financial-hacker.com. The Zorro platform can be downloaded from https://zorro-project.com.
—Petra Volkova
The Zorro Project by oP group Germany
https://zorro-project.com
BACK TO LIST

NinjaTrader: February 2025
In “Drunkard’s Walk: Theory And Measurement By Autocorrelation” in this issue, John Ehlers introduces his autocorrelation indicator. The indicator discussed in the article is available for download at the following link for NinjaTrader 8:
Once the file is downloaded, you can import the indicator into NinjaTrader 8 from within the control center by selecting Tools → Import → NinjaScript Add-On and then selecting the downloaded file for NinjaTrader 8.
You can review the indicator source code in NinjaTrader 8 by selecting the menu New → NinjaScript Editor → Indicators folder from within the control center window and selecting the file.
A sample chart is shown in Figure 6.
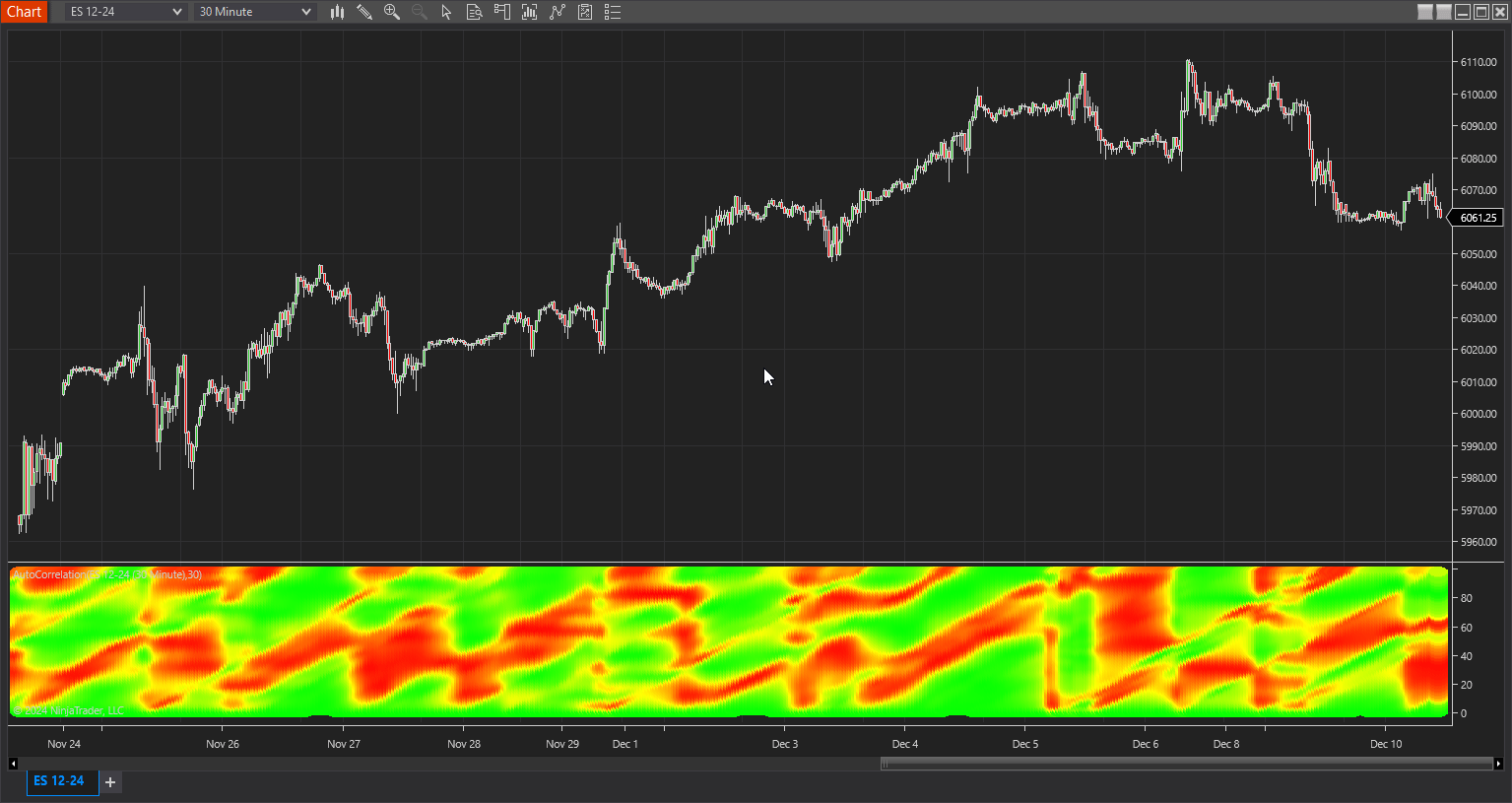
FIGURE 6: NINJATRADER. This shows an example of the indicator on a daily chart of the emini S&P 500 futures (ES).
NinjaScript uses compiled DLLs that run native, not interpreted, to provide you with the highest performance possible.
—NinjaTrader_JesseN.
NinjaTrader, LLC
www.ninjatrader.com
BACK TO LIST
Originally published in the February 2025 issue of
Technical Analysis of STOCKS & COMMODITIES magazine.
All rights reserved. © Copyright 2025, Technical Analysis, Inc.