TRADERS’ TIPS
January 2025
For this month’s Traders’ Tips, the focus is John F. Ehlers’ article in this issue, “Linear Predictive Filters And Instantaneous Frequency.” Here, we present the January 2025 Traders’ Tips code with possible implementations in various software.
You can right-click on any chart to open it in a new tab or window and view it at it’s originally supplied size, often much larger than the version printed in the magazine.
The Traders’ Tips section is provided to help the reader implement a selected technique from an article in this issue or another recent issue. The entries here are contributed by software developers or programmers for software that is capable of customization.

TradeStation: January 2025
In “Linear Predictive Filters And Instantaneous Frequency,” John Ehlers explores the use of linear predictive filters, applying the Griffiths approach and key digital signal processing principles to tackle the challenge of adaptively tuning indicators for evolving market conditions. He discusses how this approach can identify and adjust to the dominant cycle within market data.
Code in EasyLanguage for the Ehlers’ approach can be found in Ehlers article in this issue, and is also shown below.
Function: $HighPass
{
$HighPass Function
(C) 2004-2024 John F. Ehlers
}
inputs:
Price(numericseries),
Period(numericsimple);
variables:
a1( 0 ),
b1( 0 ),
c1( 0 ),
c2( 0 ),
c3( 0 );
a1 = ExpValue(-1.414 * 3.14159 / Period);
b1 = 2 * a1 * Cosine(1.414 * 180 / Period);
c2 = b1;
c3 = -a1 * a1;
c1 = (1 + c2 - c3) / 4;
if CurrentBar >= 4 then
$HighPass = c1*(Price - 2 * Price[1] + Price[2]) +
c2 * $HighPass[1] + c3 * $HighPass[2];
if Currentbar < 4 then
$HighPass = 0;
Function: $SuperSmoother
{
SuperSmoother Function
(C) 2004-2024 John F. Ehlers
}
inputs:
Price(numericseries),
Period(numericsimple);
variables:
a1( 0 ),
b1( 0 ),
c1( 0 ),
c2( 0 ),
c3( 0 );
a1 = ExpValue(-1.414 * 3.14159 / Period);
b1 = 2 * a1 * Cosine(1.414 * 180 / Period);
c2 = b1;
c3 = -a1 * a1;
c1 = 1 - c2 - c3;
if CurrentBar >= 4 then
$SuperSmoother = c1*(Price + Price[1]) / 2
+ c2 * $SuperSmoother[1] + c3 * $SuperSmoother[2];
if CurrentBar < 4 then
$SuperSmoother = Price;
Indicator: Griffiths Predictor
{
TASC JAN 2025
Griffiths Predictor Indicator
(C) 2024 John F. Ehlers
From "Rapid Measurement of Digital Instantaneous
Frequency", IEEE Transactions ASSP-23
}
inputs:
LowerBound( 18 ),
UpperBound( 40 ),
Length( 18 ),
BarsFwd( 2 );
variables:
Mu( 0 ),
HP( 0 ),
LP( 0 ),
HH( 0 ),
LL( 0 ),
Signal( 0 ),
Peak( .1 ),
XBar( 0 ),
count( 0 ),
XPred( 0 ),
Advance( 0 );
arrays:
XX[200](0),
Coef[200](0),
Pwr[200,2](0);
Mu = 1 / Length;
HP = $HighPass(Close, UpperBound);
LP = $SuperSmoother(HP, LowerBound);
Peak = .991 * Peak[1];
if AbsValue(LP) > Peak then
Peak = AbsValue(LP);
if Peak <> 0 then
Signal = LP / Peak;
//Perfect cycle test signal
//Signal = Sine(360*currentbar / 30);
for Count = 1 to Length
begin
XX[count] = Signal[Length - count];
end;
XBar = 0;
for Count = 1 to Length
begin
XBar = XBar + XX[Length - count] * Coef[count];
end;
for count = 1 to Length
begin
coef[count] = coef[count] + Mu*(XX[Length]
- XBar)*XX[Length - count];
end;
//Prediction
for Advance = 1 to BarsFwd
begin
XPred = 0;
for count = 1 to Length
begin
XPred = XPred + XX[Length + 1 - count]*coef[count];
end;
for count = advance to Length - advance
begin
XX[count] = XX[count + 1];
end;
for count = 1 to Length - 1
begin
XX[count] = XX[count + 1];
end;
XX[Length] = XPred;
end;
Plot1( Signal, "Signal" );
Plot2( 0, "Zero Line" );
Plot3( XPred, "XPred" );
Indicator: Griffiths Dominant Cycle
{
TASC JAN 2025
Griffiths Dominant Cycle Indicator
(C) 2024 John F. Ehlers
from "Rapid Measurement of Digital Instantaneous
Frequency", IEEE Transactions ASSP-23
}
inputs:
LowerBound( 18 ),
UpperBound( 40 ),
Length( 40 );
variables:
Mu( 0 ),
HP( 0 ),
LP( 0 ),
HH( 0 ),
LL( 0 ),
Signal( 0 ),
Peak( .1 ),
XBar( 0 ),
Count( 0 ),
Advance( 0 ),
Period( 0 ),
Real( 0 ),
Imag( 0 ),
Denom( 0 ),
MaxPwr( 0 ),
Cycle( 0 );
arrays:
XX[200]( 0 ),
coef[200]( 0 ),
Pwr[200,2]( 0 );
Mu = 1 / Length;
HP = $HighPass(Close, UpperBound);
LP = $SuperSmoother(HP, LowerBound);
Peak = .991*Peak[1];
if AbsValue(LP) > Peak then
Peak = AbsValue(LP);
if Peak <> 0 then
Signal = LP / Peak;
//Signal = Sine(360*currentbar / 30);
for Count = 1 to Length
begin
XX[count] = Signal[Length - count];
end;
XBar = 0;
for Count = 1 to Length
begin
XBar = XBar + XX[Length - Count] * coef[count];
end;
For count = 1 to Length
begin
coef[count] = coef[count] + Mu*(XX[Length]
- XBar) * XX[Length - count];
end;
//Instantaneous Frequency
for Period = LowerBound to UpperBound
begin
Real = 0;
Imag = 0;
for count = 1 to Length
begin
Real = Real + coef[count]
* Cosine(360*count / Period);
Imag = Imag + coef[count]
* Sine(360*count / Period);
end;
Denom = (1 - Real)*(1 - Real) + Imag*Imag;
Pwr[Period, 1] = .1 / Denom;
end;
MaxPwr = 0;
for Period = LowerBound to UpperBound
begin
If Pwr[Period, 1] > MaxPwr then
begin
MaxPwr = Pwr[Period, 1];
Cycle = Period;
end;
end;
if Cycle > Cycle[1] + 2 then
Cycle = Cycle[1] + 2;
if Cycle < Cycle[1] - 2 then
Cycle = Cycle[1] - 2;
Plot1(Cycle, "Cycle" );
Indicator: Griffiths Spectrum
{
TASC JAN 2025
Griffiths Spectrum Indicator
(C) 2024 John F. Ehlers
From "Rapid Measurement of Digitial Instantaneous
Frequency", IEEE Transactions ASSP-23
}
inputs:
LowerBound( 10 ),
UpperBound( 40 ),
Length( 40 );
variables:
Mu( 0 ) ,
HP( 0 ),
LP( 0 ),
HH( 0 ),
LL( 0 ),
Signal( 0 ),
Peak( .1 ),
XBar( 0 ),
Count( 0 ),
advance( 0 ),
Period( 0 ),
Real( 0 ),
Imag( 0 ),
Denom( 0 ),
MaxPwr( 0 ),
Color1( 0 ),
Color2( 0 ),
PlotColor( 0 );
arrays:
XX[100]( 0 ),
coef[100]( 0 ),
Pwr[100, 2]( 0 );
Mu = 1 / Length;
HP = $HighPass(Close, UpperBound);
LP = $SuperSmoother(HP, LowerBound);
Peak = .991 * Peak[1];
if AbsValue(LP) > Peak then
Peak = AbsValue(LP);
if Peak <> 0 then
Signal = LP / Peak;
for count = 1 to Length
begin
XX[count] = Signal[Length - count];
end;
XBar = 0;
for count = 1 to Length
begin
XBar = XBar + XX[Length - count]*coef[count];
end;
for count = 1 to Length
begin
coef[count] = coef[count] + Mu*(XX[Length] -
XBar)*XX[Length - count];
end;
//Instantaneous Frequency
For Period = LowerBound to UpperBound
begin
Pwr[Period, 2] = Pwr[Period, 1];
Real = 0;
Imag = 0;
for count = 1 to Length
begin
Real = Real + coef[count]
* Cosine(360 * Count / Period);
Imag = Imag + coef[count]
* Sine(360 * Count / Period);
end;
Denom = (1 - Real)*(1 - Real) + Imag*Imag;
Pwr[Period, 1] = .1 / Denom + .9*Pwr[Period, 2];
end;
MaxPwr = 0;
For Period = LowerBound to UpperBound
begin
if Pwr[Period, 1] > MaxPwr then
MaxPwr = Pwr[Period, 1];
end;
for Period = LowerBound to UpperBound
begin
if MaxPwr <> 0 then
Pwr[Period, 1] = Pwr[Period, 1] / MaxPwr;
end;
//Plot the Spectrum as a Heatmap
for Period = LowerBound to UpperBound
begin
//Convert Power to RGB Color for Display
if Pwr[Period, 1] >= .5 then
begin
Color1 = 255;
Color2 = 255*(2*Pwr[Period, 1] - 1);
end
else
begin
Color1 = 255*2*Pwr[Period, 1];
Color2 = 0;
End;
PlotColor = RGB(Color1, Color2, 0);
if period = 3 then Plot3(3, "S5", PlotColor, 0, 4);
if period = 4 then Plot4(4, "S4", PlotColor, 0, 4);
if period = 5 then Plot5(5, "S5", PlotColor, 0, 4);
if period = 6 then Plot6(6, "S6", PlotColor, 0, 4);
if period = 7 then Plot7(7, "S7", PlotColor, 0, 4);
if period = 8 then Plot8(8, "S8", PlotColor, 0, 4);
if period = 9 then Plot9(9, "S9", PlotColor, 0, 4);
if period = 10 then Plot10(10, "S10", PlotColor, 0, 4);
if period = 11 then Plot11(11, "S11", PlotColor, 0, 4);
if period = 12 then Plot12(12, "S12", PlotColor, 0, 4);
if period = 13 then Plot13(13, "S13", PlotColor, 0, 4);
if period = 14 then Plot14(14, "S14", PlotColor, 0, 4);
if period = 15 then Plot15(15, "S15", PlotColor, 0, 4);
if period = 16 then Plot16(16, "S16", PlotColor, 0, 4);
if period = 17 then Plot17(17, "S17", PlotColor, 0, 4);
if period = 18 then Plot18(18, "S18", PlotColor, 0, 4);
if period = 19 then Plot19(19, "S19", PlotColor, 0, 4);
if period = 20 then Plot20(20, "S20", PlotColor, 0, 4);
if period = 21 then Plot21(21, "S21", PlotColor, 0, 4);
if period = 22 then Plot22(22, "S22", PlotColor, 0, 4);
if period = 23 then Plot23(23, "S23", PlotColor, 0, 4);
if period = 24 then Plot24(24, "S24", PlotColor, 0, 4);
if period = 25 then Plot25(25, "S25", PlotColor, 0, 4);
if period = 26 then Plot26(26, "S26", PlotColor, 0, 4);
if period = 27 then Plot27(27, "S27", PlotColor, 0, 4);
if period = 28 then Plot28(28, "S28", PlotColor, 0, 4);
if period = 29 then Plot29(29, "S29", PlotColor, 0, 4);
if period = 30 then Plot30(30, "S30", PlotColor, 0, 4);
if period = 31 then Plot31(31, "S31", PlotColor, 0, 4);
if period = 32 then Plot32(32, "S32", PlotColor, 0, 4);
if period = 33 then Plot33(33, "S33", PlotColor, 0, 4);
if period = 34 then Plot34(34, "S34", PlotColor, 0, 4);
if period = 35 then Plot35(35, "S35", PlotColor, 0, 4);
if period = 36 then Plot36(36, "S36", PlotColor, 0, 4);
if period = 37 then Plot37(37, "S37", PlotColor, 0, 4);
if period = 38 then Plot38(38, "S38", PlotColor, 0, 4);
if period = 39 then Plot39(39, "S39", PlotColor, 0, 4);
if period = 40 then Plot40(40, "S40", PlotColor, 0, 4);
if period = 41 then Plot41(41, "S41", PlotColor, 0, 4);
if period = 42 then Plot42(42, "S42", PlotColor, 0, 4);
if period = 43 then Plot43(43, "S43", PlotColor, 0, 4);
if period = 44 then Plot44(44, "S44", PlotColor, 0, 4);
if period = 45 then Plot45(45, "S45", PlotColor, 0, 4);
if period = 46 then Plot46(46, "S46", PlotColor, 0, 4);
if period = 47 then Plot47(47, "S47", PlotColor, 0, 4);
if period = 48 then Plot48(48, "S48", PlotColor, 0, 4);
if period = 49 then Plot49(49, "S49", PlotColor, 0, 4);
if period = 50 then Plot50(50, "S50", PlotColor, 0, 4);
if period = 51 then Plot51(51, "S51", PlotColor, 0, 4);
if period = 52 then Plot52(52, "S52", PlotColor, 0, 4);
if period = 53 then Plot53(53, "S53", PlotColor, 0, 4);
if period = 54 then Plot54(54, "S54", PlotColor, 0, 4);
if period = 55 then Plot55(55, "S55", PlotColor, 0, 4);
if period = 56 then Plot56(56, "S56", PlotColor, 0, 4);
if period = 57 then Plot57(57, "S57", PlotColor, 0, 4);
if period = 58 then Plot58(58, "S58", PlotColor, 0, 4);
if period = 59 then Plot59(59, "S59", PlotColor, 0, 4);
if period = 60 then Plot60(60, "S60", PlotColor, 0, 4);
if period = 61 then Plot61(61, "S61", PlotColor, 0, 4);
if period = 62 then Plot62(62, "S62", PlotColor, 0, 4);
if period = 63 then Plot63(63, "S63", PlotColor, 0, 4);
if period = 64 then Plot64(64, "S64", PlotColor, 0, 4);
if period = 65 then Plot65(65, "S65", PlotColor, 0, 4);
if period = 66 then Plot66(66, "S66", PlotColor, 0, 4);
if period = 67 then Plot67(67, "S67", PlotColor, 0, 4);
if period = 68 then Plot68(68, "S68", PlotColor, 0, 4);
if period = 69 then Plot69(69, "S69", PlotColor, 0, 4);
if period = 70 then Plot70(70, "S70", PlotColor, 0, 4);
if period = 71 then Plot71(71, "S71", PlotColor, 0, 4);
if period = 72 then Plot72(72, "S72", PlotColor, 0, 4);
if period = 73 then Plot73(73, "S73", PlotColor, 0, 4);
if period = 74 then Plot74(74, "S74", PlotColor, 0, 4);
if period = 75 then Plot75(75, "S75", PlotColor, 0, 4);
if period = 76 then Plot76(76, "S76", PlotColor, 0, 4);
if period = 77 then Plot77(77, "S77", PlotColor, 0, 4);
if period = 78 then Plot78(78, "S78", PlotColor, 0, 4);
if period = 79 then Plot79(79, "S79", PlotColor, 0, 4);
if period = 80 then Plot80(80, "S80", PlotColor, 0, 4);
if period = 81 then Plot81(81, "S81", PlotColor, 0, 4);
if period = 82 then Plot82(82, "S82", PlotColor, 0, 4);
if period = 83 then Plot83(83, "S83", PlotColor, 0, 4);
if period = 84 then Plot84(84, "S84", PlotColor, 0, 4);
if period = 85 then Plot85(85, "S85", PlotColor, 0, 4);
if period = 86 then Plot86(86, "S86", PlotColor, 0, 4);
if period = 87 then Plot87(87, "S87", PlotColor, 0, 4);
if period = 88 then Plot88(88, "S88", PlotColor, 0, 4);
if period = 89 then Plot89(89, "S89", PlotColor, 0, 4);
if period = 90 then Plot90(90, "S90", PlotColor, 0, 4);
if period = 91 then Plot91(91, "S91", PlotColor, 0, 4);
if period = 92 then Plot92(92, "S92", PlotColor, 0, 4);
if period = 93 then Plot93(93, "S93", PlotColor, 0, 4);
if period = 94 then Plot94(94, "S94", PlotColor, 0, 4);
if period = 95 then Plot95(95, "S95", PlotColor, 0, 4);
if period = 96 then Plot96(96, "S96", PlotColor, 0, 4);
if period = 97 then Plot97(97, "S97", PlotColor, 0, 4);
if period = 98 then Plot98(98, "S98", PlotColor, 0, 4);
if period = 99 then Plot99(99, "S99", PlotColor, 0, 4);
end;
A sample chart is shown in Figure 1.
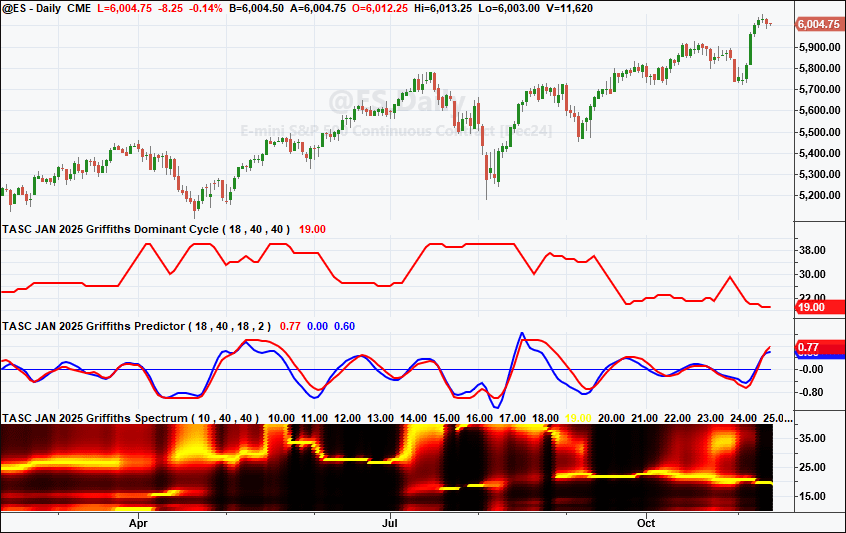
FIGURE 1: TRADESTATION. This shows a daily chart of the continuous emini S&P 500 showing a portion of 2024 with all three indicators applied.
This article is for informational purposes. No type of trading or investment recommendation, advice, or strategy is being made, given, or in any manner provided by TradeStation Securities or its affiliates.
—John Robinson
TradeStation Securities, Inc.
www.TradeStation.com
BACK TO LIST

Wealth-Lab.com: January 2025
Leave it John Ehlers to remind former electrical engineers how much we’ve forgotten! In “Linear Predictive Filters And Instantaneous Frequency” in this issue, Ehlers uses the Griffiths approach with elements of digital signal processing to offer coding for some indicators to help solve the challenge of adaptively tuning indicators and strategy algorithms to the dominant cycle of the data. The article includes several code listings to calculate and plot the indicators on a chart. Just to translate all the code presented in the article took the better part of a day, but the result is worth it.
Atop the Griffiths spectrum in Figure 2, you’ll see the “white hot” dominant cycle (DC) indicator snapping to the frequency with the most energy. Note however that it’s constrained to change only by two cycles per bar to prevent “bouncing.” The heat map is primarily eye candy (useful to impress your spouse and friends), but the Griffith DC indicator is the key to “adaptively tune indicators and strategy algorithms,” as Ehlers states in his article. The GriffithsDC and GriffithsPredictor indicators can now be found in our WealthLab.TASC indicator library.
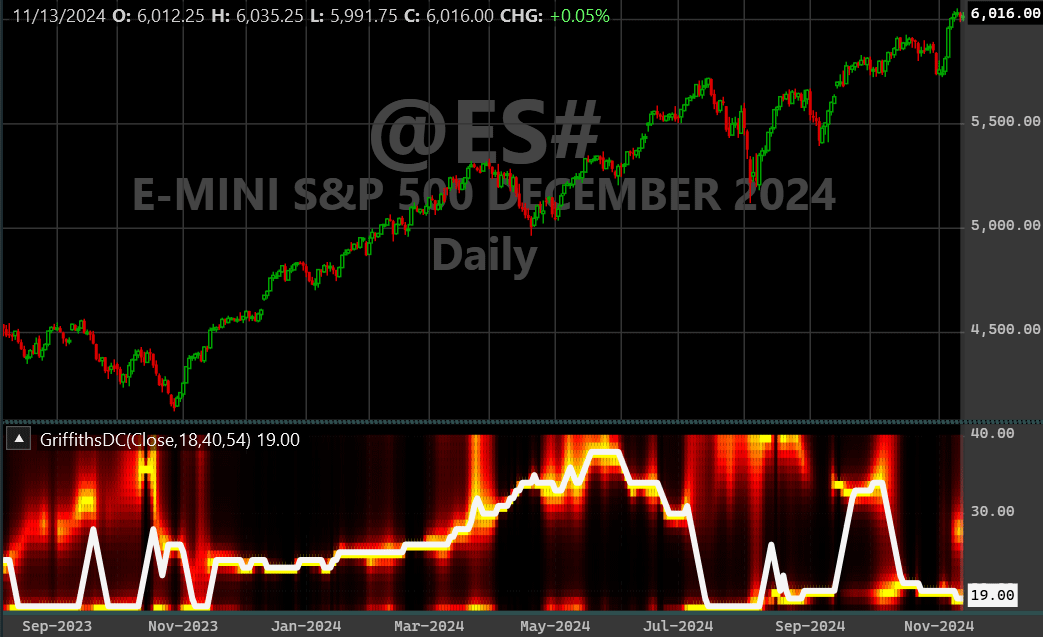
FIGURE 2: WEALTH-LAB. This example daily chart of the emini S&P 500 futures (ES) displays the Griffiths spectrum with the dominant cycle indicator. The GriffithsDC and GriffithsPredictor indicators can now be found in the WealthLab.TASC indicator library.
using System;
using WealthLab.Backtest;
using WealthLab.Core;
using WealthLab.TASC;
namespace WealthScript
{
public class GriffithSpectrum : UserStrategyBase
{
Parameter _ub, _lb, _length;
public GriffithSpectrum()
{
_lb = AddParameter("Lowerbound", ParameterType.Int32, 18, 5, 40, 5);
_ub = AddParameter("Upperbound", ParameterType.Int32, 40, 20, 125, 5);
_length = AddParameter("Length", ParameterType.Int32, 54, 30, 60, 1);
}
public override void Initialize(BarHistory bars)
{
TimeSeries ds = bars.Close;
int ubound = _ub.AsInt;
if (ubound > ds.Count) ubound = ds.Count;
//initialize raster series
SetPaneDrawingOptions("GrSp", 20);
int nser = ubound - _lb.AsInt + 1;
TimeSeries[] Raster = new TimeSeries[nser];
for (int n = 0; n < nser; n++)
{
Raster[n] = new TimeSeries(bars.DateTimes, n + _lb.AsInt);
PlotTimeSeriesLine(Raster[n], "", "GrSp", WLColor.Black, 8, suppressLabels:true);
}
double[] XX = new double[_length.AsInt];
double[] coef = new double[_length.AsInt];
double[,] Pwr = new double[nser, 2];
int L1 = _length.AsInt - 1;
double Mu = 1.0 / _length.AsInt;
TimeSeries HP = new HighPass(ds, ubound);
TimeSeries LP = new SuperSmoother(HP, _lb.AsInt);
TimeSeries Peak = new TimeSeries(ds.DateTimes, 0.1);
TimeSeries Signal = new TimeSeries(ds.DateTimes, 0);
for (int bar = Math.Max(ubound, _length.AsInt); bar < ds.Count; bar++)
{
Peak[bar] = 0.991 * Peak[bar - 1];
if (Math.Abs(LP[bar]) > Peak[bar])
Peak[bar] = Math.Abs(LP[bar]);
Signal[bar] = Peak[bar] != 0 ? LP[bar] / Peak[bar] : Signal[bar - 1];
for (int count = 0; count < _length.AsInt; count++)
XX[count] = Signal[bar - (L1 - count)];
double XBar = 0;
for (int count = 0; count < _length.AsInt; count++)
XBar += XX[L1 - count] * coef[count];
for (int count = 0; count < _length.AsInt; count++)
coef[count] += Mu * (XX[L1] - XBar) * XX[L1 - count];
//instantaneous frequency
for (int pidx = 0; pidx < nser; pidx++)
{
double period = pidx + _lb.AsInt;
Pwr[pidx, 1] = Pwr[pidx, 0];
double real = 0;
double imag = 0;
for (int count = 0; count < _length.AsInt; count++)
{
real += coef[count] * Math.Cos(2 * Math.PI * count / period);
imag += coef[count] * Math.Sin(2 * Math.PI * count / period);
}
double denom = (1 - real) * (1 - real) + imag * imag;
Pwr[pidx, 0] = 0.1 / denom + 0.9 * Pwr[pidx, 1];
}
double maxPwr = 0;
for (int pidx = 0; pidx < nser; pidx++)
if (Pwr[pidx, 0] > maxPwr)
maxPwr = Pwr[pidx, 0];
for (int pidx = 0; pidx < nser; pidx++)
if (maxPwr != 0) Pwr[pidx, 0] = Pwr[pidx, 0] / maxPwr;
//convert power to RGB color
for (int pidx = 0; pidx < nser; pidx++)
{
double clr1 = Pwr[pidx, 0] >= 0.5 ? 255 : 255 * 2 * Pwr[pidx, 0];
double clr2 = Pwr[pidx, 0] >= 0.5 ? 255 * (2 * Pwr[pidx, 0] - 1) : 0;
SetSeriesBarColor(Raster[pidx], bar, WLColor.FromRgb((byte)clr1, (byte)clr2, 0));
}
}
//Plot the Dominant Cycle
GriffithsDC gdc = GriffithsDC.Series(ds, _lb.AsInt, _ub.AsInt, _length.AsInt);
PlotTimeSeriesLine(gdc, gdc.Description, "GrSp", WLColor.WhiteSmoke, 4);
}
public override void Execute(BarHistory bars, int idx)
{ }
}
}
—Robert Sucher
Wealth-Lab team
www.wealth-lab.com
BACK TO LIST

NeuroShell Trader: January 2025
The highpass, SuperSmoother, 2-pole predictor and Griffiths indicators presented in John Ehlers’ article in this issue, In “Linear Predictive Filters And Instantaneous Frequency,” can be easily implemented in NeuroShell Trader using NeuroShell Trader’s ability to call external dynamic linked libraries (DLLs). Dynamic linked libraries can be written in C, C++ and Power Basic.
After moving the code given in the article to your preferred compiler and creating a DLL, you can insert the resulting indicator as follows:
- Select “new indicator” from the insert menu.
- Choose the External Program & Library Calls category.
- Select the appropriate External DLL Call indicator.
- Set up the parameters to match your DLL.
- Select the finished button.
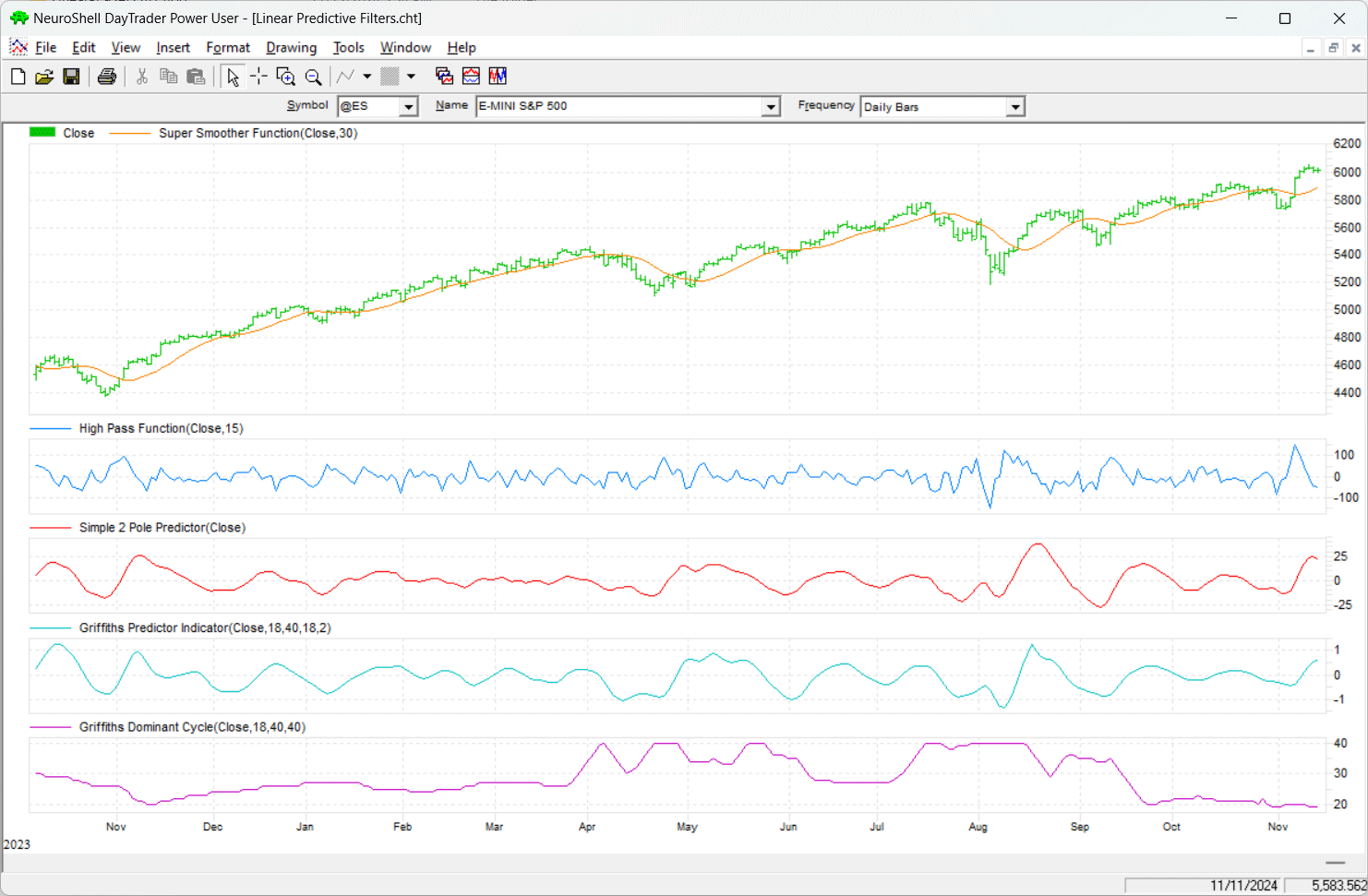
FIGURE 3: NEUROSHELL TRADER. This NeuroShell Trader chart shows the highpass, SuperSmoother, 2-pole predictor, Griffiths predictor, and Griffiths dominant cyle on a chart of the S&P Emini futures (ES).
Users of NeuroShell Trader can go to the Stocks & Commodities section of the NeuroShell Trader free technical support website to download a copy of this or any previous Traders’ Tips.
—Ward Systems Group, Inc.
sales@wardsystems.com
www.neuroshell.com
BACK TO LIST
TradingView: January 2025
The TradingView Pine Script code presented here implements the Griffiths predictor, Griffiths dominant cycle indicator, and Griffiths spectrum, as discussed in John Ehlers’ article in this issue, “Linear Predictive Filters And Instantaneous Frequency.”
// TASC Issue: January 2025
// Article: Linear Predictive Filters And
// Instantaneous Frequency
// Article By: John F. Ehlers
// Language: TradingView's Pine Script™ v5
// Provided By: PineCoders, for tradingview.com
//@version=5
title ='TASC 2025.01 Linear Predictive Filters'
stitle = 'LPF'
indicator(title, stitle, false)
//#region Inputs and Constants:
// @variable Overload for plot `display.all`.
DSPA = display.all
// @variable Overload for plot `display.none`.
DSPN = display.none
// @variable Overload for plot style `plot.style_columns`.
PSH = plot.style_columns
// @variable Full Angle Rotation `360`.
float FROT = 2.0 * math.pi
// @variable Square Root of 2 `1.414`.
float SQRT2 = math.sqrt(2.0)
// @variable Perfect Cycle Test signal.
// `Signal = math.sin(360.0 * bar_index / 30.0)`.
float TS = math.sin(FROT * bar_index / 30.0)
// @enum Indicator Display Choice Enumerator.
enum eID
SMP = 'Simple 2-Pole Predictor'
GP = 'Griffiths Predictor'
GS = 'Griffiths Spectrum'
GD = 'Griffiths Dominant Cycle'
GSD = 'Griffiths Spectrum and Dominant Cycle'
// @variable Indicator Display Choice.
eID iChoice = input.enum(eID.SMP, 'Select Indicator:')
// @variable Use Test Signal.
bool iTest = input.bool(false, 'Use Test Signal:')
// Parameters:
float Src = input.source(close, 'Source:')
int LBound = input.int(18, 'Lower Bound:')
int UBound = input.int(40, 'Upper Bound:')
int Length = input.int(40, 'Length:')
float Q = input.float(0.35, 'Simple Predictor Q:')
int BarsF = input.int(2,'Griffiths Predictor Bars Forward:')
//#endregion
//#region Filter functions
// @function High Pass Filter.
HP (float Source, int Period) =>
float a0 = math.pi * math.sqrt(2.0) / Period
float a1 = math.exp(-a0)
float c2 = 2.0 * a1 * math.cos(a0)
float c3 = -a1 * a1
float c1 = (1.0 + c2 - c3) * 0.25
float hp = 0.0
if bar_index >= 4
hp := c1 * (Source - 2.0 * Source[1] + Source[2]) +
c2 * nz(hp[1]) + c3 * nz(hp[2])
hp
// @function Super Smoother
SS (float Source, int Period) =>
float a0 = math.pi * math.sqrt(2.0) / Period
float a1 = math.exp(-a0)
float c2 = 2.0 * a1 * math.cos(a0)
float c3 = -a1 * a1
float c1 = 1.0 - c2 - c3
float ss = Source
if bar_index >= 4
ss := c1 * ((Source + Source[1]) / 2.0) +
c2 * nz(ss[1]) + c3 * nz(ss[2])
ss
// @function Common function.
CF (float Source=close, int LowerB=18, int UpperB=40,
bool Test=false ) =>
float HP = HP(Source, UpperB)
float LP = SS(HP, LowerB)
float Peak = 0.1
Peak := .991 * nz(Peak[1])
if math.abs(LP) > Peak
Peak := math.abs(LP)
if Test
TS
else
float Signal = 0.0
if Peak != 0.0
Signal := LP / Peak
Signal
//#endregion
//#region Simple 2 Pole Predictor
SP (float Source=close, int lengthHP=15, int lengthLP=30,
float Q=0.35, bool Test=false) =>
float HP = HP(Source, lengthHP)
float LP = SS(HP, lengthLP)
float Signal = Test ? TS : LP
float c0 = 1.0 , float c1 = 1.8 * Q , float c2 = -Q * Q
float sum = 1.0 - c1 - c2
c0 := (c0 / sum) * Signal
c1 := (c1 / sum) * Signal[1]
c2 := (c2 / sum) * Signal[2]
float Predict = c0 - c1 - c2
[Signal, Predict]
//#endregion
//#region Griffiths Predictor
GP (float source=close, int lowerB=18, int upperB=40,
int length=18, int barsF=2, bool Test=false) =>
float MU = 1.0 / length
float Signal = CF(source, lowerB, upperB, Test)
float[] XX = array.new<float>(length+1, 0.0)
var float[] Coef = array.new<float>(length+1, 0.0)
float XBar = 0.0
XX.set(length, Signal)
for count = 1 to length - 1
XX.set(count, nz(Signal[length - count]))
for count = 1 to length
XBar += XX.get(length-count) * Coef.get(count)
for count = 1 to length
Coef.set(count, Coef.get(count) +
MU * (XX.get(length) - XBar) *
XX.get(length-count))
// Prediction
float XPred = 0.0
for advance = 1 to barsF
XPred := 0.0
for count = 1 to length
XPred += XX.get(length+1-count)*Coef.get(count)
for count = advance to length - advance
XX.set(count, XX.get(count + 1))
for count = 1 to length - 1
XX.set(count, XX.get(count + 1))
XX.set(length, XPred)
[Signal, XPred]
//#endregion
//#region Griffiths Spectrum
GS (float source=close, int lowerB=10, int upperB=40,
int length=40, bool Test=false) =>
int LP1 = length + 1 , float MU = 1.0 / length
float Signal = CF(source, lowerB, upperB, Test)
float[] XX = array.new<float>(LP1, 0.0)
var float[] Coef = array.new<float>(LP1, 0.0)
var matrix<float> Pwr = matrix.new<float>(LP1, 2, 0.0)
float XBar = 0.0
XX.set(length, Signal)
for count = 1 to length - 1
XX.set(count, nz(Signal[length - count]))
for count = 1 to length
XBar += XX.get(length-count) * Coef.get(count)
for count = 1 to length
Coef.set(count, Coef.get(count) +
MU * (XX.get(length) - XBar) *
XX.get(length-count))
// Instantaneous Frequency
for period = lowerB to upperB
Pwr.set(period, 1, Pwr.get(period, 0))
float re = 0.0 , float im = 0.0
for count = 1 to length
float a0 = FROT * count / period
re += Coef.get(count) * math.cos(a0)
im += Coef.get(count) * math.sin(a0)
denom = math.pow(1.0 - re, 2.0) + math.pow(im, 2.0)
Pwr.set(period, 0, 0.1 / denom)
float MaxPwr = Pwr.col(0).max()
if MaxPwr != 0
for period = lowerB to upperB
Pwr.set(period, 0, Pwr.get(period, 0) / MaxPwr)
// Plot the Spectrum Colors
color[] Spectrum = array.new<color>(100, #000000)
for period = lowerB to upperB
// Convert Power to RGB Color for display
float p0 = Pwr.get(period, 0)
float r = p0 >= 0.5 ? 255.0 : 255.0 * 2.0 * p0
float g = p0 >= 0.5 ? 255.0 * (2.0 * p0 - 1.0) : 0.0
Spectrum.set(period, color.rgb(r, g, 0.0))
Spectrum
//#endregion
//#region Griffiths Dominant Cycle
GD (float source=close, int lowerB=18, int upperB=40,
int length=40, bool Test=false) =>
int LP1 = length + 1 , float MU = 1.0 / length
float Signal = CF(source, lowerB, upperB, Test)
float[] XX = array.new<float>(LP1, 0.0)
var float[] Coef = array.new<float>(LP1, 0.0)
var matrix<float> Pwr = matrix.new<float>(LP1, 2, 0.0)
float XBar = 0.0
XX.set(length, Signal)
for count = 1 to length - 1
XX.set(count, nz(Signal[length - count]))
for count = 1 to length
XBar += XX.get(length-count) * Coef.get(count)
for count = 1 to length
Coef.set(count, Coef.get(count) +
MU * (XX.get(length) - XBar) *
XX.get(length-count))
// Instantaneous Frequency
for period = lowerB to upperB
Pwr.set(period, 1, Pwr.get(period, 0))
float re = 0.0 , float im = 0.0
for count = 1 to length
float a0 = FROT * count / period
re += Coef.get(count) * math.cos(a0)
im += Coef.get(count) * math.sin(a0)
denom = math.pow(1.0 - re, 2.0) + math.pow(im, 2.0)
// float _p1 = Pwr.get(period, 1)
Pwr.set(period, 0, 0.1 / denom)// + 0.9 * _p1)
float MaxPwr = Pwr.col(0).max()
float cycle = Pwr.col(0).indexof(MaxPwr)
cycle := switch
cycle >= cycle[1] + 2.0 => cycle[1] + 2.0
cycle <= cycle[1] - 2.0 => cycle[1] - 2.0
=> cycle
cycle
//#endregion
//#region Plots:
// Indicator IO Conditionals:
D0 = iChoice == eID.SMP ? DSPA : DSPN
D1 = iChoice == eID.GP ? DSPA : DSPN
D2 = iChoice == eID.GS or iChoice == eID.GSD ? DSPA : DSPN
D3 = iChoice == eID.GD or iChoice == eID.GSD ? DSPA : DSPN
// Simple 2-Pole Predictor
[s1, p1] = SP(Src, LBound, UBound, 0.35, iTest)
plot(s1, 'Signal', color.blue, display=D0)
hline(0, display=D0)
plot(p1, 'Predict', color.red, display=D0)
// Griffiths Predictor
[s2, p2] = GP(Src, LBound, UBound, Length, 2, iTest)
plot(s2, 'Signal', color.blue, display=D1)
hline(0, display=D1)
plot(p2, 'Predict', color.red, display=D1)
// Griffiths Spectrum
SP = GS(Src, LBound, UBound, Length, iTest)
plot(19, '', SP.get(18), 1, PSH, false, 18, display=D2)
plot(20, '', SP.get(19), 1, PSH, false, 19, display=D2)
plot(21, '', SP.get(20), 1, PSH, false, 20, display=D2)
plot(22, '', SP.get(21), 1, PSH, false, 21, display=D2)
plot(23, '', SP.get(22), 1, PSH, false, 22, display=D2)
plot(24, '', SP.get(23), 1, PSH, false, 23, display=D2)
plot(25, '', SP.get(24), 1, PSH, false, 24, display=D2)
plot(26, '', SP.get(25), 1, PSH, false, 25, display=D2)
plot(27, '', SP.get(26), 1, PSH, false, 26, display=D2)
plot(28, '', SP.get(27), 1, PSH, false, 27, display=D2)
plot(29, '', SP.get(28), 1, PSH, false, 28, display=D2)
plot(30, '', SP.get(29), 1, PSH, false, 29, display=D2)
plot(31, '', SP.get(30), 1, PSH, false, 30, display=D2)
plot(32, '', SP.get(31), 1, PSH, false, 31, display=D2)
plot(33, '', SP.get(32), 1, PSH, false, 32, display=D2)
plot(34, '', SP.get(33), 1, PSH, false, 33, display=D2)
plot(35, '', SP.get(34), 1, PSH, false, 34, display=D2)
plot(36, '', SP.get(35), 1, PSH, false, 35, display=D2)
plot(37, '', SP.get(36), 1, PSH, false, 36, display=D2)
plot(38, '', SP.get(37), 1, PSH, false, 37, display=D2)
plot(39, '', SP.get(38), 1, PSH, false, 38, display=D2)
plot(40, '', SP.get(39), 1, PSH, false, 39, display=D2)
// Griffiths Dominant Cycle
cycle = GD(Src, LBound, UBound, Length, iTest)
plot(cycle, 'Dominant Cycle', color.blue, 3, display=D3)
//#endregion
The indicator is available on TradingView from the PineCodersTASC account: https://www.tradingview.com/u/PineCodersTASC/#published-scripts.
An example chart is shown in Figure 4.
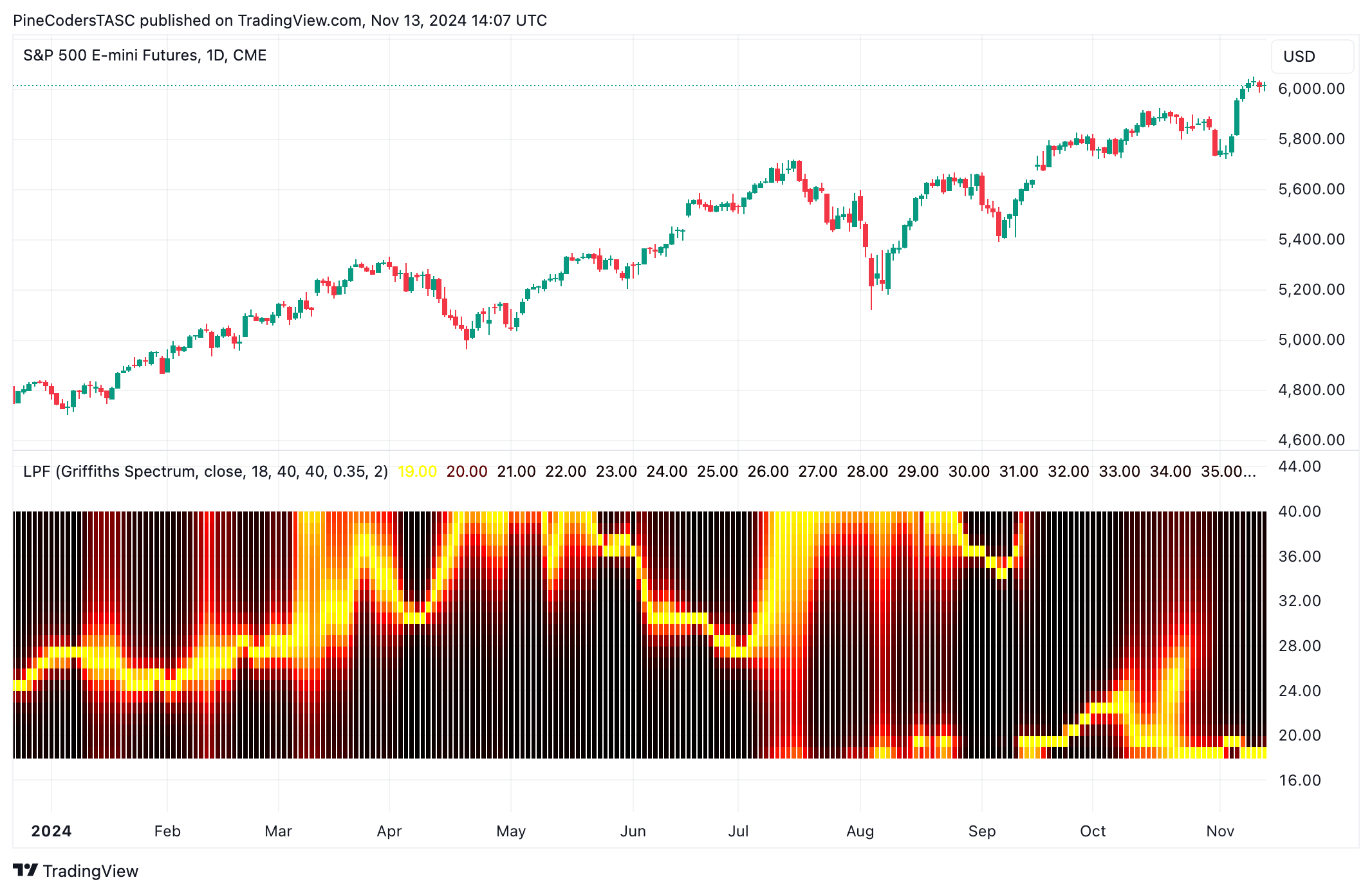
FIGURE 4: TRADINGVIEW. Here is an example of the indicator and heatmap on a daily chart of the emini S&P 500 futures (ES).
—PineCoders, for TradingView
https://TradingView.com
BACK TO LIST

NinjaTrader: January 2025
In the article “Linear Predictive Filters And Instantaneous Frequency” in this issue, John Ehlers discusses some digital signal processing techniques and an approach using Griffiths spectrum. Several of the indicators discussed in the article are available for download at the following link for NinjaTrader 8:
www.ninjatrader.com/SC/January2025SCNT8.zip
Once the file is downloaded, you can import it into NinjaTrader 8 from within the control center by selecting Tools → Import → NinjaScript Add-On and then selecting the downloaded file for NinjaTrader 8.
You can review the source code in NinjaTrader 8 by selecting the menu New → NinjaScript Editor → Indicators folder from within the control center window and selecting the file.
NinjaScript uses compiled DLLs that run native, not interpreted, to provide you with the highest performance possible.
—Chelsea Bell
NinjaTrader, LLC
www.ninjatrader.com
BACK TO LIST
Originally published in the January 2025 issue of
Technical Analysis of STOCKS & COMMODITIES magazine.
All rights reserved. © Copyright 2024, Technical Analysis, Inc.